使用PyTorch求解RTE(和Matlab代码对比)
Contents
使用PyTorch求解RTE(和Matlab代码对比)#
下面是一段求解RTE方程的Matlab代码,我们将以此为例,逐步将其用Pytorch进行实现。
% it solves the multiscale heat transfer based on the phonon Boltzmann transport equation
% by using the synthetic iteration scheme
% the BTE are given by Phys. Rev. E 96 (2017) 063311, but the macroscopic
% acceleration equation is different. In fact, our macroscopic equation is
% derived exactly from the BTE
% Initial condition
a = 1;
c = 1;
rho = 1;
cv = 1;
fileIDI0 = fopen('I0.txt', 'w');
fileIDT = fopen('T.txt','w');
% ini = sin(2 * pi * x)
% spatial grid
N=400;
L = 1;
dx = L / N;
x = 0.5 * dx : dx : L - 0.5 * dx;
Tini = 0.1 * sin(2 * pi * x) + 1;
sigma = 1;
CFL = 0.8;
dt=CFL*dx; % time step
dtc = dt * c;
ddtc = 1/ dtc;
% velocity grid & angle
Nvx=8;
[mu, wmu] = Get_Gauss_Point(Nvx);
% distribution function
T = Tini;
I = zeros(Nvx, N + 2);
I(:, 2:end-1) = repmat(0.5 * a * c * Tini.^4, Nvx, 1);
I(:,1)=I(:, end-1); I(:,end)=I(:,2); % boundary condition
I0 = wmu' * I; % energe
%% main iteration
for loop=1: 1/dt
I_out = I;
T_out = T;
I0_out = I0;
%% streaming, positive vx
lv=Nvx/2+1:Nvx;coe = mu(lv); index = 2:N + 1;
I(lv, index) = I_out(lv, index) ...
- dt / dx * coe .* (I_out(lv, index) - I_out(lv, index -1))...
+ dt * sigma * (0.5*a*c * repmat(T_out.^4, Nvx/2, 1) - I_out(lv, index));
%% streaming, negative vx
lv=1:Nvx/2; coe= mu(lv);
I(lv,index)= I_out(lv, index) ...
-dt / dx * coe .* (I_out(lv, index+1) - I_out(lv, index))...
+ dt * sigma * (0.5*a*c * repmat(T_out.^4, Nvx/2,1) - I_out(lv, index));
%% macroscopic quantities
I(:,end)= I(:, 2); I(:,1)= I(:, end-1);
T = T_out + dt / cv * sigma .* (I0_out(index) - a * c * T_out.^4);
I0 = wmu' * I;
loop
fprintf(fileIDI0, '%12.8f',I0(2:end-1));
fprintf(fileIDT, '%12.8f',T);
fprintf(fileIDT, '\n');
fprintf(fileIDI0, '\n');
end
fclose(fileIDI0);
fclose(fileIDT);
function [points, weight] = Get_Gauss_Point(n)
syms x
f = legendreP(n, x);
points = sort(double(solve(f==0)));
tmpf = diff(f, x);
tmpf = subs(tmpf, 'x', points);
weight = double(2 ./ (1 - points.^2) ./ (tmpf.^2));
end
导入用到的包#
import torch
import numpy as np
import torch.nn.functional as F
import matplotlib.pyplot as plt
辅助函数 get_gauss_point#
在matlab中,我们使用
function [points, weight] = Get_Gauss_Point(n)
syms x
f = legendreP(n, x);
points = sort(double(solve(f==0)));
tmpf = diff(f, x);
tmpf = subs(tmpf, 'x', points);
weight = double(2 ./ (1 - points.^2) ./ (tmpf.^2));
end
获取积分节点和权重
def get_gauss_point(n):
x, w = np.polynomial.legendre.leggauss(n)
return torch.from_numpy(x).to(dtype=torch.get_default_dtype()), torch.from_numpy(w).to(dtype=torch.get_default_dtype())
定义问题参数#
% Initial condition
a = 1;
c = 1;
rho = 1;
cv = 1;
a = 1
c = 1
rho = 1
cv = 1
打开文件#
fileIDI0 = fopen('I0.txt', 'w');
fileIDT = fopen('T.txt','w');
fileIDI0 = open('I0.txt', 'w')
fileIDT = open('T.txt','w')
定义空间网格,设定初值#
N=400;
L = 1;
dx = L / N;
x = 0.5 * dx : dx : L - 0.5 * dx;
Tini = 0.1 * sin(2 * pi * x) + 1;
sigma = 1;
CFL = 0.8;
dt=CFL*dx; % time step
dtc = dt * c;
ddtc = 1/ dtc;
下面是对应的Python代码
# spatial grid
N = 400
L = 1
dx = L / N
x = torch.arange(0.5 * dx, L + 0.5 * dx, dx)
Tini = 1 + 0.1 * torch.sin(2 * np.pi * x)
sigma = 1 + 0.1 * torch.sin(2 * np.pi * x)
CFL = 0.8
dt = CFL * dx # time step
dtc = dt * c
ddtc = 1 / dtc
分布函数初值#
% velocity grid & angle
Nvx=8;
[mu, wmu] = Get_Gauss_Point(Nvx);
% distribution function
T = Tini;
I = zeros(Nvx, N + 2);
I(:, 2:end-1) = repmat(0.5 * a * c * Tini.^4, Nvx, 1);
I(:,1)=I(:, end-1); I(:,end)=I(:,2); % boundary condition
I0 = wmu' * I; % energe
# velocity grid & angle
Nvx = 8
mu, wmu = get_gauss_point(Nvx)
# distribution function
T = Tini
I = 0.5 * a * c * Tini**4
I = I.repeat(Nvx, 1)
I = F.pad(I[None, ...], (1, 1), mode='circular')[0]
Flux=torch.zeros((Nvx,N+1))
I0 = wmu @ I # energe
sigma = sigma.repeat(Nvx // 2, 1)
主循环#
for loop=1: 1/dt
I_out = I;
T_out = T;
I0_out = I0;
%% streaming, positive vx
lv=Nvx/2+1:Nvx;coe = mu(lv); index = 2:N + 1;
I(lv, index) = I_out(lv, index) ...
- dt / dx * coe .* (I_out(lv, index) - I_out(lv, index -1))...
+ dt * sigma * (0.5*a*c * repmat(T_out.^4, Nvx/2, 1) - I_out(lv, index));
%% streaming, negative vx
lv=1:Nvx/2; coe= mu(lv);
I(lv,index)= I_out(lv, index) ...
-dt / dx * coe .* (I_out(lv, index+1) - I_out(lv, index))...
+ dt * sigma * (0.5*a*c * repmat(T_out.^4, Nvx/2,1) - I_out(lv, index));
%% macroscopic quantities
I(:,end)= I(:, 2); I(:,1)= I(:, end-1);
T = T_out + dt / cv * sigma .* (I0_out(index) - a * c * T_out.^4);
I0 = wmu' * I;
loop
fprintf(fileIDI0, '%12.8f',I0(2:end-1));
fprintf(fileIDT, '%12.8f',T);
fprintf(fileIDT, '\n');
fprintf(fileIDI0, '\n');
end
for loop in range(int(1 / dt)): #=1: 1/dt
I_out = I.clone()
T_out = T.clone()
I0_out = I0.clone()
index = slice(1, -1)
index_add1 = slice(2, None)
index_sub1 = slice(None, -2)
# streaming, positive vx
lv = slice(Nvx // 2, None)
coe = mu[lv]
I[lv, index] = I_out[lv, index] - dt / dx * coe[..., None] * (
I_out[lv, index] - I_out[lv, index_sub1]) + dt * sigma * (
(0.5 * a * c * T_out**4).repeat(Nvx // 2, 1) - I_out[lv, index])
# streaming, negative vx
lv = slice(0, Nvx // 2)
coe = mu[lv]
I[lv, index] = I_out[lv, index] - dt / dx * coe[..., None] * (
I_out[lv, index_add1] - I_out[lv, index]) + dt * sigma * (
(0.5 * a * c * T_out**4).repeat(Nvx // 2, 1) - I_out[lv, index])
I = F.pad(I[None, ..., 1:-1], (1, 1), mode='circular')[0]
T = T_out + dt / cv * sigma[0, :] * (I0_out[index] - a * c * T_out**4)
I0 = wmu @ I
fileIDI0.write(str(I0.numpy())+"\n")
fileIDT.write(str(T.numpy())+"\n")
关闭文件#
fclose(fileIDI0);
fclose(fileIDT);
fileIDI0.close()
fileIDT.close()
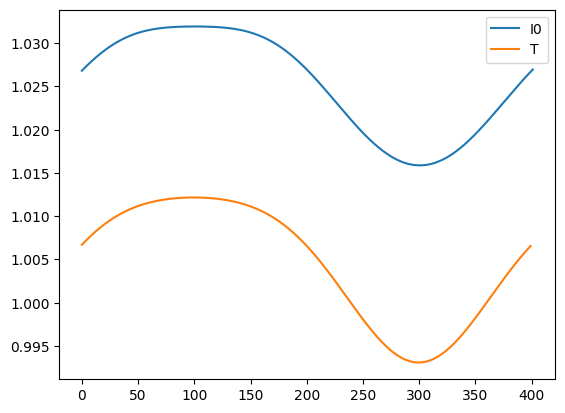
结果可视化#
plt.plot(I0,label="I0")
plt.plot(T,label="T")
plt.legend()
<matplotlib.legend.Legend at 0x7f639b558ee0>
为什么要用PyTorch实现?#
CUDA加速
函数变换
自动微分
融合神经网络
…


