Fourier neural operator
Contents
Fourier neural operator#
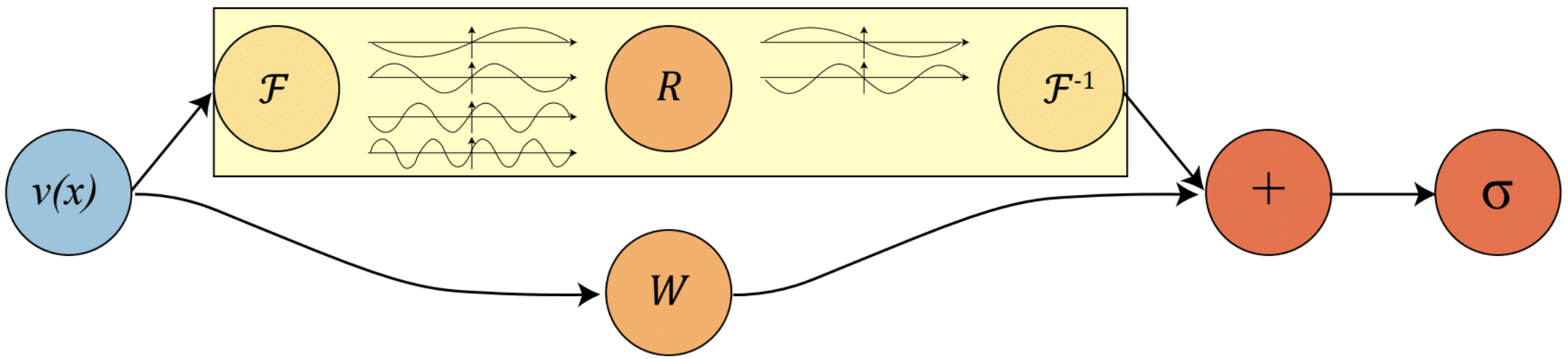
网络结构#
import torch
from torch import nn
from functools import partial
import torch.nn.functional as F
下面我们首先定义FNO中的单个block,也就是上图中的黄框部分
################################################################
# 1d fourier layer
################################################################
class SpectralConv1d(nn.Module):
def __init__(self, in_channels, out_channels, modes):
super(SpectralConv1d, self).__init__()
"""
1D Fourier layer. It does FFT, linear transform, and Inverse FFT.
"""
self.in_channels = in_channels
self.out_channels = out_channels
self.modes = modes # Number of Fourier modes to multiply, at most floor(N/2) + 1
self.scale = 1 / (in_channels * out_channels)
self.weights = nn.Parameter(
self.scale * torch.rand(in_channels, out_channels, self.modes, dtype=torch.cfloat)
)
def forward(self, x):
# Compute Fourier coeffcients up to factor of e^(- something constant)
x_ft = torch.fft.rfft(x, dim=-1, norm="ortho")
# Multiply relevant Fourier modes
# (batch, in_channel, x ), (in_channel, out_channel, x) -> (batch, out_channel, x)
out_ft = torch.zeros(
x.shape[0], self.in_channels, x.size(-1) + 1, device=x.device, dtype=torch.cfloat)
out_ft[:, :, : self.modes] = torch.einsum("bix,iox->box",x_ft[:, :, : self.modes],self.weights)
# Return to physical space
x = torch.fft.irfft(out_ft, dim=-1, n=x.size(-1), norm="ortho")
return x
然后一个完成FNO的一个block,这有若干个Fourier卷积和普通卷积组合而成。
class SimpleBlock1d(nn.Module):
def __init__(self, inchannel, outchannel, modes, width, padding_mode, activation):
super(SimpleBlock1d, self).__init__()
"""
The overall network. It contains 4 layers of the Fourier layer.
1. Lift the input to the desire channel dimension by self.fc0 .
2. 4 layers of the integral operators u' = (W + K)(u).
W defined by self.w; K defined by self.conv .
3. Project from the channel space to the output space by self.fc1 and self.fc2 .
input: the solution of the initial condition and location (a(x), x)
input shape: (batchsize, x=s, c=2)
output: the solution of a later timestep
output shape: (batchsize, x=s, c=1)
"""
self.modes = modes
self.width = width
self.inchannel = inchannel
self.outchannel = outchannel
self.padding_mode = padding_mode
self.fc0 = nn.Linear(
self.inchannel, self.width
) # input channel is 2: (a(x), x)
self.conv0 = SpectralConv1d(self.width, self.width, self.modes)
self.conv1 = SpectralConv1d(self.width, self.width, self.modes)
self.conv2 = SpectralConv1d(self.width, self.width, self.modes)
self.conv3 = SpectralConv1d(self.width, self.width, self.modes)
self.w0 = nn.Conv1d(self.width, self.width, 1)
self.w1 = nn.Conv1d(self.width, self.width, 1)
self.w2 = nn.Conv1d(self.width, self.width, 1)
self.w3 = nn.Conv1d(self.width, self.width, 1)
self.fc1 = nn.Linear(self.width, 128)
self.fc2 = nn.Linear(128, self.outchannel)
self.act=getattr(torch.nn, activation)()
def forward(self, x):
x = self.fc0(x)
x = x.permute(0, 2, 1)
x1 = self.conv0(x)
x2 = self.w0(x)
x = x1 + x2
x = self.act(x)
x1 = self.conv1(x)
x2 = self.w1(x)
x = x1 + x2
x = self.act(x)
x1 = self.conv2(x)
x2 = self.w2(x)
x = x1 + x2
x = self.act(x)
x1 = self.conv3(x)
x2 = self.w3(x)
x = x1 + x2
x = x.permute(0, 2, 1)
x = self.fc1(x)
x = self.act(x)
x = self.fc2(x)
return x
最后,一个FNO由若干个FNO块组成,我们这里选取最简单的由单块组成的网络。
class FNO1d(nn.Module):
def __init__(
self,
in_channel=5,
out_channel=1,
modes=32,
hidden=64,
padding_mode="circular",
activation="ReLU",
):
super(FNO1d, self).__init__()
self.conv1 = SimpleBlock1d(
in_channel,
out_channel,
modes,
width=hidden,
padding_mode=padding_mode,
activation=activation,
)
def forward(self, x):
x = self.conv1(x)
return x
至此,我们已经完成了FNO网络结构的定义。下面就是找一些数据来测试FNO的效果。我们使用之前写好的RTE求解器生成500组数据。
import math
import numpy as np
from torch.func import vmap
import torch.nn.functional as F
def get_gauss_point(n):
x, w = np.polynomial.legendre.leggauss(n)
return torch.from_numpy(x).to(dtype=torch.get_default_dtype()), torch.from_numpy(w).to(dtype=torch.get_default_dtype())
a = 1
c = 1
rho = 1
cv = 1
# spatial grid
N = 400
L = 1
dx = L / N
x = torch.arange(0.5 * dx, L + 0.5 * dx, dx)
Tini = vmap(lambda cas:(1 + 0.1 * torch.sin(2 * math.pi * x * (1+cas%2) +torch.sin(cas)))*(1+torch.sin(cas)))(torch.arange(500))
sigma = vmap(lambda cas:(1 + 0.1 * torch.sin(2 * math.pi * x * (1+cas%2) +torch.sin(cas+1)))*(1+torch.sin(cas)))(torch.arange(500))
def solve(Tini,sigma):
CFL = 0.8
dt = CFL * dx # time step
dtc = dt * c
ddtc = 1 / dtc
datarecord_sigma=sigma.clone()[None,:]
# velocity grid & angle
Nvx = 8
mu, wmu = get_gauss_point(Nvx)
# distribution function
T = Tini
I = 0.5 * a * c * Tini**4
I = I.repeat(Nvx, 1)
I = F.pad(I[None, ...], (1, 1), mode='circular')[0]
I0 = wmu @ I # energe
sigma = sigma.repeat(Nvx // 2, 1)
t=1.0
Nt=int(t / dt)
list_T=[]
list_E=[]
for loop in range(Nt): #=1: 1/dt
I_out = I.clone()
T_out = T.clone()
I0_out = I0.clone()
index = slice(1, -1)
index_add1 = slice(2, None)
index_sub1 = slice(None, -2)
# streaming, positive vx
lv = slice(Nvx // 2, None)
coe = mu[lv]
I[lv, index] = I_out[lv, index] - dt / dx * coe[..., None] * (
I_out[lv, index] - I_out[lv, index_sub1]) + dt * sigma * (
(0.5 * a * c * T_out**4).repeat(Nvx // 2, 1) - I_out[lv, index])
# streaming, negative vx
lv = slice(0, Nvx // 2)
coe = mu[lv]
I[lv, index] = I_out[lv, index] - dt / dx * coe[..., None] * (
I_out[lv, index_add1] - I_out[lv, index]) + dt * sigma * (
(0.5 * a * c * T_out**4).repeat(Nvx // 2, 1) - I_out[lv, index])
I = F.pad(I[None, ..., 1:-1], (1, 1), mode='circular')[0]
T = T_out + dt / cv * sigma[0, :] * (I0_out[index] - a * c * T_out**4)
I0 = wmu @ I
if loop%10==0:
list_E.append(I0[...,1:-1].clone())
list_T.append(T.clone())
datarecord_E=torch.stack(list_E,dim=0)
datarecord_T=torch.stack(list_T,dim=0)
return datarecord_E,datarecord_T,datarecord_sigma
E,T,sigma=vmap(solve)(Tini,sigma)
print(E.shape,T.shape,sigma.shape)
torch.Size([500, 50, 400]) torch.Size([500, 50, 400]) torch.Size([500, 1, 400])
然后我们将其包装成数据集,我们令输入是0时刻的E,T以及参数sigma,输出的是最后时刻的E和T. 我们这里对数据进行标准化。
x_data=torch.stack([E[:,0],T[:,0],sigma.expand_as(E)[:,0]],dim=-1)
y_data=torch.stack([E[:,-1],T[:,-1]],dim=-1)
x_data=(x_data-x_data.mean(dim=(0,1),keepdims=True))/x_data.std(dim=(0,1),keepdims=True)
y_data=(y_data-y_data.mean(dim=(0,1),keepdims=True))/y_data.std(dim=(0,1),keepdims=True)
print(f"{x_data.shape=},{y_data.shape=}")
x_train,y_train=x_data[:-20],y_data[:-20]
x_valid,y_valid=x_data[-20:],y_data[-20:]
train_dataset=torch.utils.data.TensorDataset(x_train,y_train)
valid_dataset=torch.utils.data.TensorDataset(x_valid,y_valid)
x_data.shape=torch.Size([500, 400, 3]),y_data.shape=torch.Size([500, 400, 2])
训练网络#
train_dataloader=torch.utils.data.DataLoader(train_dataset,batch_size=64,shuffle=True,num_workers=2)
valid_dataloader=torch.utils.data.DataLoader(valid_dataset,batch_size=64,shuffle=False,num_workers=2)
myFNO=FNO1d(3,2)
#myFNO.cuda()
optimizer=torch.optim.Adam(myFNO.parameters(), lr=1e-3)
scheduler=torch.optim.lr_scheduler.CosineAnnealingWarmRestarts(optimizer,100,2)
epochs=300
train_loss_hist=[]
valid_loss_hist=[]
for i in range(1,1+epochs):
train_loss=0
for x,y in train_dataloader:
#x,y=x.cuda(),y.cuda()
y_pred=myFNO(x)
loss=(y_pred-y).square().mean()
train_loss+=loss.item()
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss_hist.append(train_loss/480)
scheduler.step()
valid_loss=0
for x,y in valid_dataloader:
#x,y=x.cuda(),y.cuda()
y_pred=myFNO(x)
loss=(y_pred-y).square().mean()
valid_loss+=loss.item()
optimizer.zero_grad()
loss.backward()
optimizer.step()
valid_loss_hist.append(valid_loss/20)
if i%10==0:
print(f"epoch:{i}, train loss: {train_loss}, valid loss: {valid_loss}")
epoch:10, train loss: 0.003175586462020874, valid loss: 0.00037672792677767575
epoch:20, train loss: 0.0002588716615719022, valid loss: 3.065231430809945e-05
epoch:30, train loss: 9.93086869129911e-05, valid loss: 1.1333598195051309e-05
epoch:40, train loss: 5.538810160032881e-05, valid loss: 6.490697160188574e-06
epoch:50, train loss: 2.024030345637584e-05, valid loss: 2.717382585615269e-06
epoch:60, train loss: 1.244708732883737e-05, valid loss: 1.421161186954123e-06
epoch:70, train loss: 9.589616411176394e-06, valid loss: 1.1114556173197343e-06
epoch:80, train loss: 8.339804935530992e-06, valid loss: 9.134378728958836e-07
epoch:90, train loss: 8.066567716014106e-06, valid loss: 8.570763725401775e-07
epoch:100, train loss: 7.9013756248969e-06, valid loss: 8.48483011850476e-07
epoch:110, train loss: 3.975824483859469e-05, valid loss: 2.010224670812022e-05
epoch:120, train loss: 0.00029864934731449466, valid loss: 7.92315840953961e-05
epoch:130, train loss: 0.00010102950159307511, valid loss: 1.3228697753220331e-05
epoch:140, train loss: 1.3250306039935822e-05, valid loss: 1.4218400110621587e-06
epoch:150, train loss: 7.340786112308706e-06, valid loss: 6.053697916286183e-07
epoch:160, train loss: 1.137120779048928e-05, valid loss: 5.193124366087432e-07
epoch:170, train loss: 3.7670119468202756e-06, valid loss: 5.149904040990805e-07
epoch:180, train loss: 2.3749674085138395e-06, valid loss: 3.525242675550544e-07
epoch:190, train loss: 2.419967600530981e-06, valid loss: 3.263542396325647e-07
epoch:200, train loss: 1.7950417401380037e-06, valid loss: 2.044468772055552e-07
epoch:210, train loss: 1.4594621120522788e-06, valid loss: 1.6817412529235298e-07
epoch:220, train loss: 1.4386312159331283e-06, valid loss: 1.286770867636733e-07
epoch:230, train loss: 1.3689481193068787e-06, valid loss: 1.538402614187362e-07
epoch:240, train loss: 1.2285119623811624e-06, valid loss: 1.2656184367187961e-07
epoch:250, train loss: 1.176968879690321e-06, valid loss: 1.2355535261576733e-07
epoch:260, train loss: 1.1003755133742743e-06, valid loss: 1.0413278772603007e-07
epoch:270, train loss: 1.1253409724076846e-06, valid loss: 9.877408047032077e-08
epoch:280, train loss: 1.0549202897891519e-06, valid loss: 1.047883415594697e-07
epoch:290, train loss: 1.034728200011159e-06, valid loss: 9.921025423409446e-08
epoch:300, train loss: 1.0490981381394704e-06, valid loss: 9.879754259145557e-08
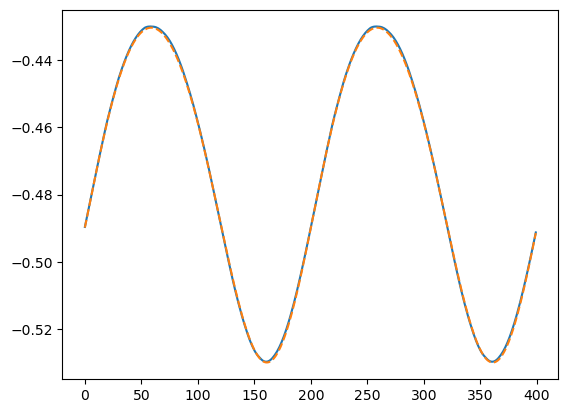
可视化结果#
import matplotlib.pyplot as plt
y_pred=myFNO(x_valid)
plt.plot(y_pred[1,:,1].detach().cpu())
plt.plot(y_valid[1,:,1],"--")
[<matplotlib.lines.Line2D at 0x7f2744212d40>]