摘要
本文作者来自著名有限元分析软件开发商Ansys公司,提出了一种基于机器学习的NS方程求解器。
Method
DiscretizationNet可以用来求解 steady, incompressible Navier-Stokes equations \[ \left\{ \begin{array}{**lr**} \nabla \cdot \boldsymbol v=0 \\ (\boldsymbol v \cdot \nabla)\boldsymbol v+\nabla p-\frac{1}{Re}\nabla^2 v=0 \end{array} \right. \] 其中\(\boldsymbol v =(u,v,w)\),\(\boldsymbol p\)是scaled pressure。
网络结构
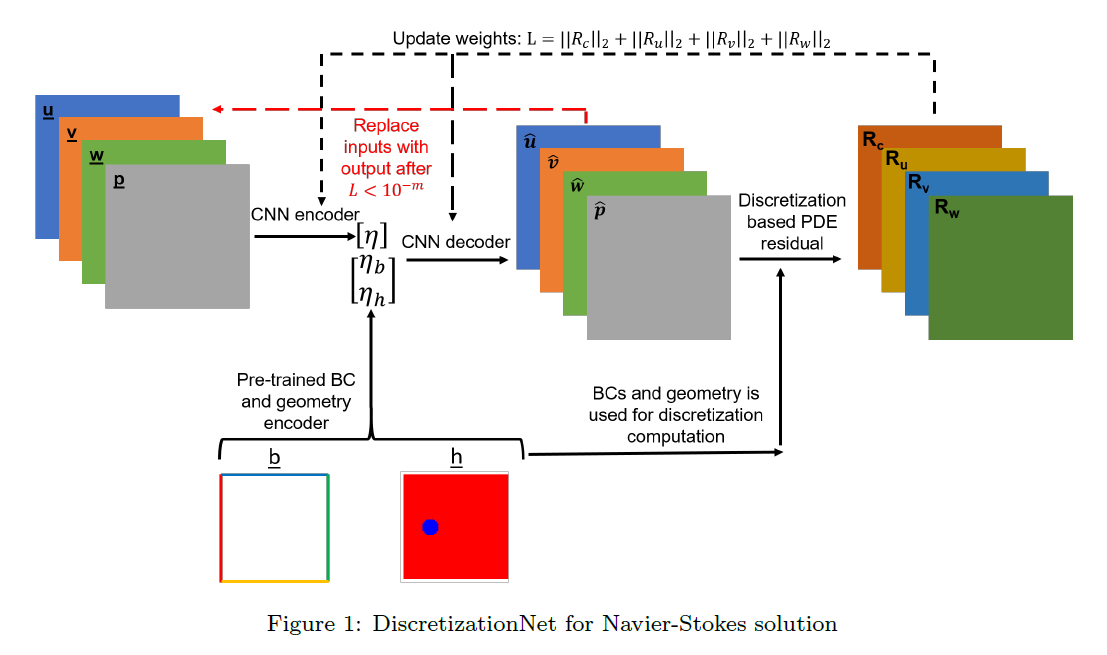
有一个Encode-Decoder网络,接受物理量(\(u,v,w,p\))的输入(solution space大小),输出同样尺度的物理量,希望输出的物理量比输入的物理量更接近方程的真解。其中encoder给出的latent space中的物理量要和 边界条件和geometry coder输出的code一起提供给decoder。相当于一个conditional autoencoder。
随后使用某种数值方法,例如有限体积法(文章中提到如果需要高阶精度,也可以用Finite Element Method (FEM), Discontinuous Galerkin (DG) ,此处用FVM是为了方便GPU并行加速)计算decoder输出的物理量在方程中的残差。
Training Mechanics
传统的生成器网络可能会输入随机变量和condition vector,输出解,这样可能不太好训练,因为输出数据是一个随机变量的函数。
所以作者使用迭代的方法,每次decoder-encoder输入的是上次的输出。
训练的目的是通过极小化PDE残差生成方程的解,同时学习解的latent space。
如图,每次用Loss的梯度对encoder和decoder进行梯度下降即可。
我们可以注意到,每次训练网络时是data free的,也就是我们不需要PDE的真解,只需要每次计算PDE的残差即可。
Geometry and Boundary encoder
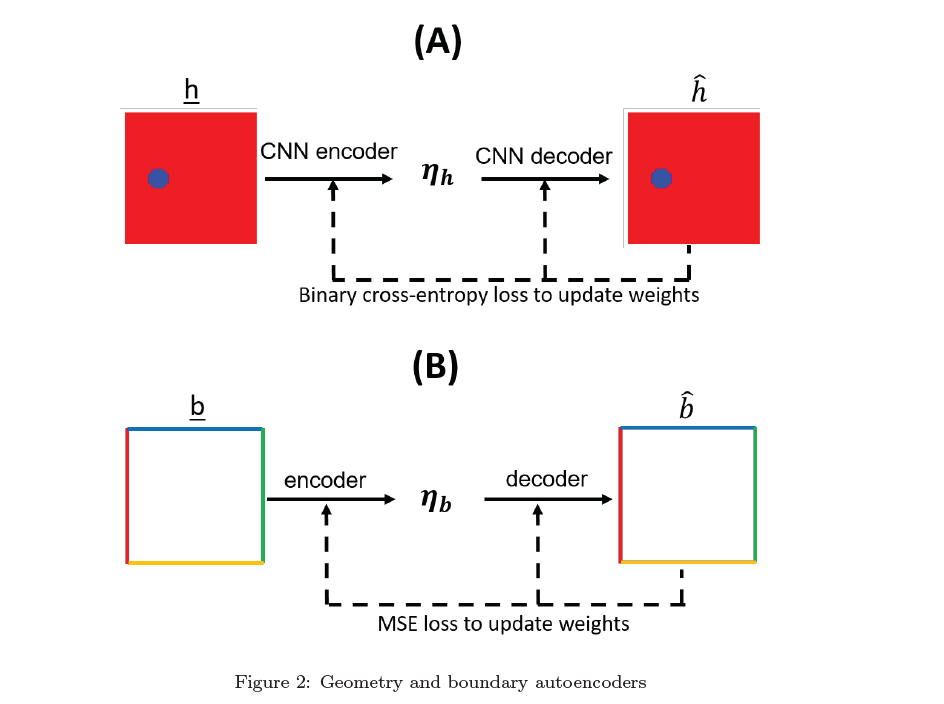
对于几何形状和边界条件的encoder也很简单,就是一个autoencoder,在训练主网络(PDE求解器)之前pre train一下。
此外,Raynold数或者Prandtl数也可以视作边界条件,和边界条件的code一起供给decoder。
Loss
\[ \lambda(W,b)=||\lambda_c||_{\Omega}+||\lambda_u||_{\Omega}+||\lambda_v||_{\Omega}+||\lambda_w||_{\Omega} \]
\(||\lambda_c||_{\Omega},||\lambda_u||_{\Omega},||\lambda_v||_{\Omega},||\lambda_w||_{\Omega}\)分别表示continuity,和x,y,z方向动量的残差的L-2 norm。
Inference for other geometry and boundary conditions
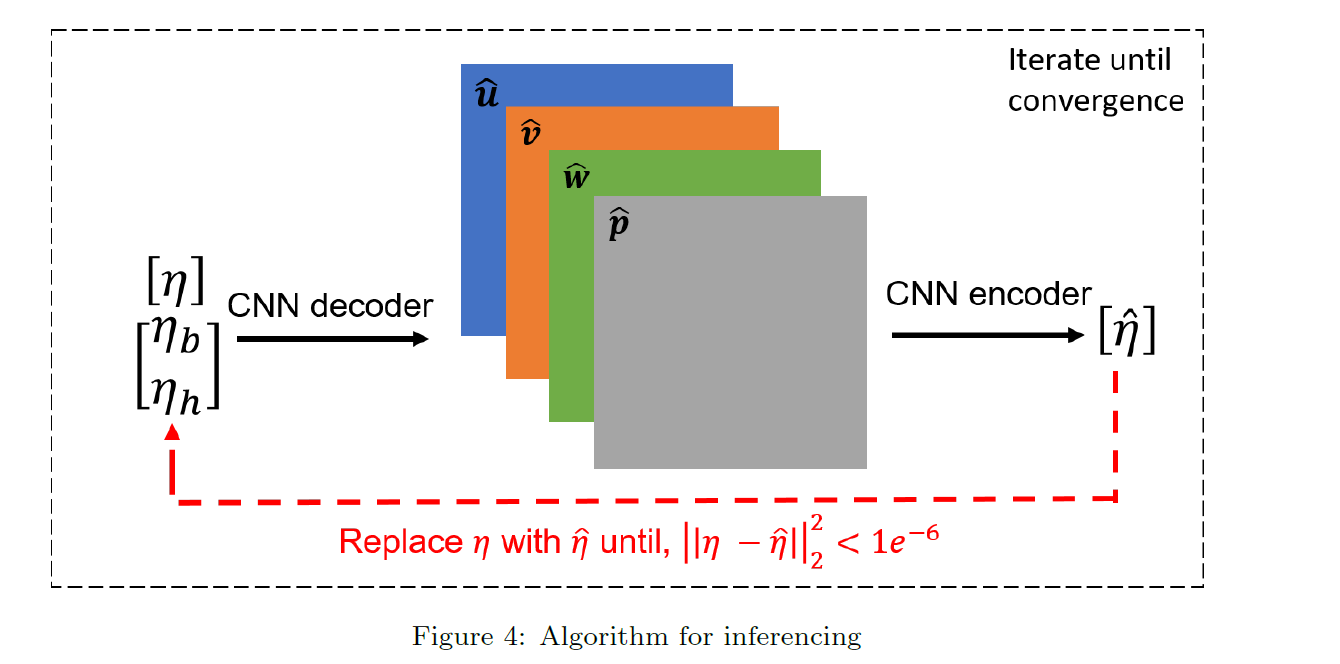
这部分最关键,就是训练好的网络如何拿来求解不同边值条件的NS方程。
因为我们训练网络时就用了不同的边值条件来训练,所以我们的网络自然而然的具有一定泛化性,可以求解不同边值条件的方程。我们先生成随机的初值,然后喂进网络里,取得输出再次输入,反复迭代,直到输出和输入基本一致时停止。此时的输入/输出值就是方程的解。
实验结果和结论
在以下三个案例中测试了 ML-solver 求解 the 3-D steady,incompressible Navier-Stokes equations
lid-driven cavity,
lamina row past a cylinder
conjugate heat transfer.
结果显示和 ANSYS Fluent R19.3 有很好的一致性。
训练中使用不到30000步即可收敛,每步用时不到1s(在NVIDIA Tesla V100 SXM2 GPU.)。
实验结果中既展示了在训练集中的边界条件的解,在网络训练完成后,收敛到了接近真解的状态;也展示了不在训练集中的边界条件,在使用训练好的网络进行推断时,也能推断出好的解。但是测试的数据基本是训练数据的一种内插,即使用\(\{0.2,0.4,0.6,0.8\}\)的参数训练,测试0.5,和使用\(\{8,20\}\)训练,测试13。所以网络的泛化性可能有一定限制,不是对于所有的边界条件都用一个网络都能解决。但是对于相近的边界条件训练一个网络就可能足够了。
作者提出可以使用LSTM扩展ML-solver使得其能求解unsteady的问题。