看见汤老师微博上的一个问题,感觉很有趣,查了一下相关资料,总结如下。
问题是这样的: 
看起来结果很不可思议,但是知道原理后又令人觉得理所应当。
首先,这个积分形式就是故意遮去一半,试图让人不往傅里叶变换的方向去想,所以我们就用傅里叶变换来解。直接把积分区域翻倍到实轴上,例如
\[ \begin{equation} \int_{-\infty}^{\infty} \frac{\sin t}{t} \frac{\sin(t/101)}{t/101} \frac{\sin(t/201)}{t/201}dt=\pi \label{eq1} \end{equation} \]
我们记
\[ sinc(t)=\frac{\sin t}{t} \]
注意到\(sinc(t)\)的傅里叶变换是
\[ \begin{equation} \mathcal F (sinc(t))=F(x)= \left\{ \begin{aligned} 1/2 \quad|x| < 1 \\ 0 \quad|x| > 1 \end{aligned} \right. \end{equation} \]
我们现在对()做傅里叶变换。傅里叶变换下乘积变卷积:
\[ \begin{equation} \frac{1}{2\pi}\int_{-\infty}^{\infty} f(t)g(t)e^{-j2 \pi xt}dt=F(x)*G(x) \label{eq2} \end{equation} \]
更一般的
\[ \begin{equation} \frac{1}{2\pi}\int_{-\infty}^{\infty} f_1(t)f_2(t)...f_n(t)e^{-j2 \pi xt}dt=F_1(x)*F_2(x)*...*F_n(x) \label{eq3} \end{equation} \]
取\(x=0\)求得的就是我们想要的。下面一张动图展示了\(F=F_1*F_2*...*F_n\)在0处的值。
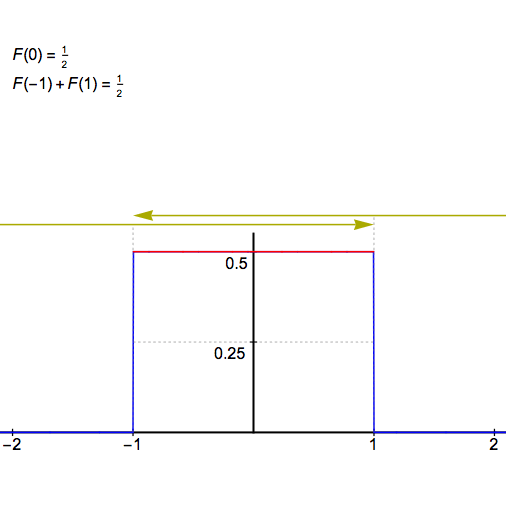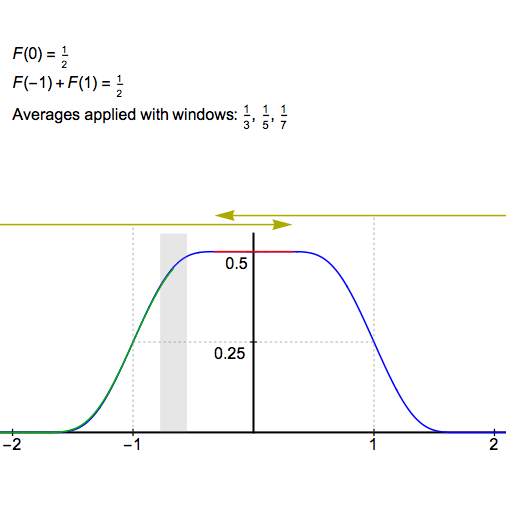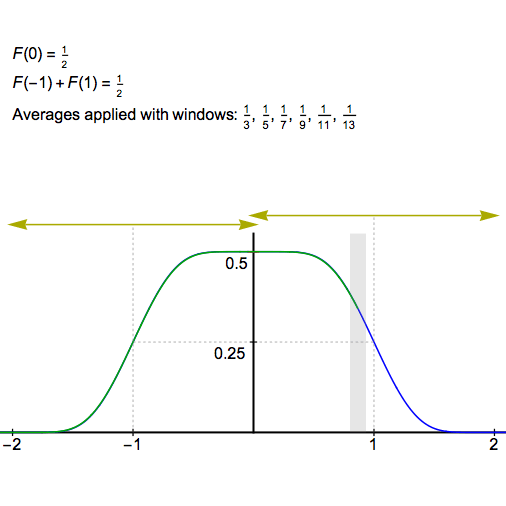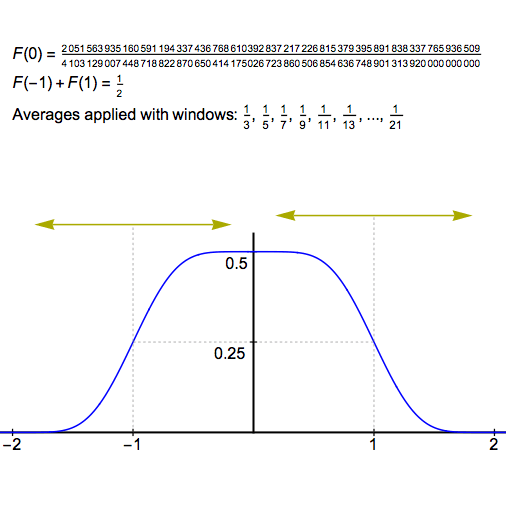
\(F_0=\mathcal F (sinc(t))\)是一个高为\(1/2\),半宽为1的矩形波。\(F_k=\mathcal F (sinc(t/{a_k}))\)是高为\(1/2\),半宽为\(a_k\)的矩形波。
\(F_0\)与\(F_{k}\)做卷积后,两个函数分别在 保持等于\(1/2\)的横线的半宽度就缩小了\(a_k\)。再卷积\(F_{k+1}\),半宽度就缩小了\(a_{k+1}\)。这段长度的值为\(\sum_{k=1}^{n} a_k\)。 注意除了中间这一段横线的值依然保持等于\(1/2\),其余区域的函数值是严格小于\(1/2\)的。
当\(\sum_{k=1}^{n} a_k>1\)时,就不存在值为1的线段了,所有函数值都小于\(\pi\)了。
所以这道题的结论到这里就清晰了,当\(n<9.8*10^42\)时,\(\sum_{k=1}^{n} 1/(100k+1)<1\);当\(n>7.4*10^43\)时,\(\sum_{k=1}^{n} 1/(100k+1)>1\)。这样就出现了题目所示的“神奇现象”。